Wave, Sound, and Music

Polarization

Transverse wave has a special property called polarization. As shown in Figure 08a, if the current (e.g., in the antenna) is oscillating along a fixed direction, the electric field E will oscillate in the same direction, while the associated magnetic field B

		will oscillate in a perpendicular direction. Thermal radiation emitting from large number of incoherent sources (molecules) is unpolarized. Only the radiations from organized motion such as those in antenna transmission, laser, or accelerating electron beam (as in synchrotron radiation) exhibit this polarization effect. Since the electric field can always be resolved into two components perpendicular to each other, in many situations one of these components would be blocked or the optical paths separated by the interacting material. Figure 08b
Figure 08a Polarization [view large image]	Figure 08b Polarized Light [view large image]	shows the polarization of unpolarized light by reflection (glare), scattering (blue sky, red sunset), transmission (through Polaroid filter), and double refraction (in some crystals such as calcite).

		More detailed analysis of the electromagnetic radiation shows that there are actually two independent oscillating E fields with polarization vectors ₁ and ₂ perpendicular to each other as shown in Figure 08c, where k is in the direction of propagation perpendicular to both ₁ and ₂. These two E fields can be combined to form: E(x,t) = (E₁₁ + E₂₂) e^{i(kz - t)} ---------- (7a)
Figure 08c EM Polarization [view large image]	Figure 08d Circular Polarization [view large image]	If E₁ = E₂ = E₀ and have the same phase, then E(x,t) = E₀ e^{i(kz - t)}, where = ₁ + ₂, represents the linear polarization as in Figure 08a.

If E₁ = E₂ = E₀, but differ in phase by 90^o, then Eq.(7a) becomes:

E(x,t) = E₀(₁ i₂) e^{i(kz - t}). ---------- (7b)

When the z axis is aligned to the direction of k, and ₁, ₂ are in the x and y directions respectively, it can be shown that

E_x = E_o cos(kz -

t) ---------- (7c)

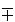E_y = E₀ sin(kz -

t) ---------- (7d)

For any instant of time, for example, t = 0, Eqs.(7c) and (7d) trace out a circular helix. Figure 08d shows the spatial pattern of circular polarization. The vector E rotates in a circle either counter-clockwise or clockwise according to the

sign - it is also referred as right-handed or left-handed helicity respectively. For the more general case of E₁

E₂, and there is a phase difference, the time variation of the vector E will trace out the elliptical trajectory (at a fixed z, e.g., z = 0) as shown in Figure 08e, where

/2 is related to the phase difference. This is called elliptical polarization.

Figure 08e Elliptical Polarization

See more in "Electromagnetic Wave Polarization and Photon Spin".