
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 i instead of ak, and the identity matrix as I instead of b) :
i instead of ak, and the identity matrix as I instead of b) : | ---------- (25) |
 +
+ 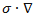 )][i(
)][i( -
- 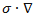 )]u = m2u ---------- (26)
)]u = m2u ---------- (26)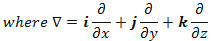 ;
;| u = | 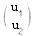 | ---------- (27a) |
| v = | 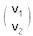 | ---------- (27b) |
Figure 02e Dirac Equation [view large image] |
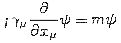 | ---------- (29a) |
 i and the 4-components field (usually known as Dirac spinor)
i and the 4-components field (usually known as Dirac spinor)  are expressed in the forms :
are expressed in the forms :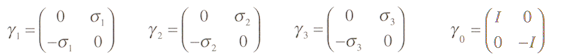
 | ---------- (29b) |