 |
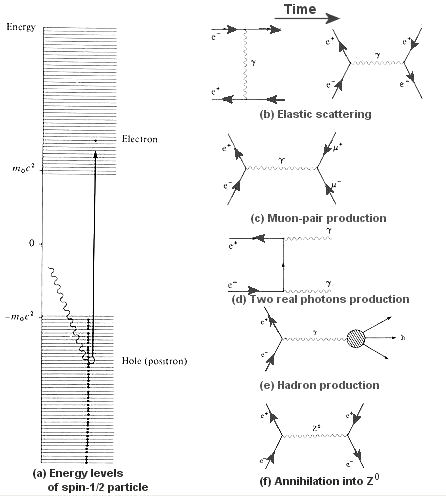
To get around the problem of negative energy, Dirac proposed an energy spectrum containing all electrons in the universe (see Figure 03). In addition to the normal positive-energy spectrum, it also contains the negative-energy variety, which spans the spectrum from -m0c2 down to negative infinity. All the negative-energy levels are filled, thus the positive-energy particle is inhibited from transition into these lower energy states bypassing the unobserved phenomena of falling into the negative energy levels. Thus, the existence of negative energy has no observable effect in the real world. Only when there is enough energy available, e.g., when E  2moc2, a real particle and anti-particle pair with positive-energy can be created from this unseen sea of negative-energy particles. The particle is the electron originally resided in the negative energy region, while the anti-particle (positron) can be interpreted as the hole in the vacated energy level acquiring a mass mo. The law of charge conservation demands that this anti-particle carries a positive charge. Many interesting things occur when the electron meets the hole (see Figure 03). Over the past three 2moc2, a real particle and anti-particle pair with positive-energy can be created from this unseen sea of negative-energy particles. The particle is the electron originally resided in the negative energy region, while the anti-particle (positron) can be interpreted as the hole in the vacated energy level acquiring a mass mo. The law of charge conservation demands that this anti-particle carries a positive charge. Many interesting things occur when the electron meets the hole (see Figure 03). Over the past three |
|
decades, the use of e+e- collisions to probe the vacuum have yielded a great deal of information about the nature of the strong, weak, and electromagnetic interactions, and have played a major role in establishing the Standard Model of |

 2moc2, a real particle and anti-particle pair with positive-energy can be created from this unseen sea of negative-energy particles. The particle is the electron originally resided in the negative energy region, while the anti-particle (positron) can be interpreted as the hole in the vacated energy level acquiring a mass mo. The law of charge conservation demands that this anti-particle carries a positive charge. Many interesting things occur when the electron meets the hole (see Figure 03). Over the past three
2moc2, a real particle and anti-particle pair with positive-energy can be created from this unseen sea of negative-energy particles. The particle is the electron originally resided in the negative energy region, while the anti-particle (positron) can be interpreted as the hole in the vacated energy level acquiring a mass mo. The law of charge conservation demands that this anti-particle carries a positive charge. Many interesting things occur when the electron meets the hole (see Figure 03). Over the past three 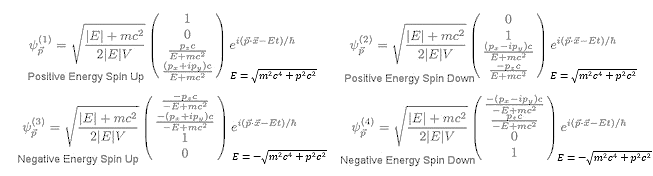
 *
*
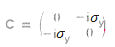
 C
C  /2 for 4 to 1, 2 to 3, and 0 for 3 to 2, 1 to 4.
It can be shown that the eigenvalue for this charge conjugation operator C is c =
/2 for 4 to 1, 2 to 3, and 0 for 3 to 2, 1 to 4.
It can be shown that the eigenvalue for this charge conjugation operator C is c =  1.
1. 
 /2 while the entire magnetic moment precesses around the field with a magnitude S = [(s+1)s]1/2 (Figure 04). The expression for the magnetic moment derived in quantum theory has the form:
/2 while the entire magnetic moment precesses around the field with a magnitude S = [(s+1)s]1/2 (Figure 04). The expression for the magnetic moment derived in quantum theory has the form:  x +
x + 
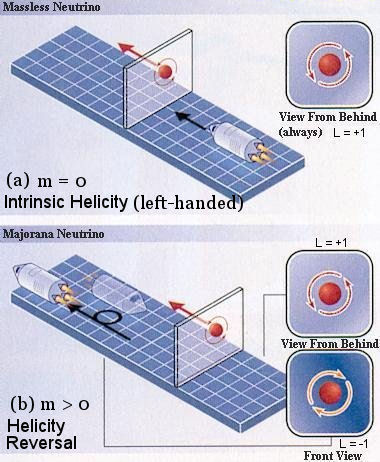

 such that R => e-i
such that R => e-i