 |
Geometry is defined as the mathematics of shapes: the branch of mathematics that is concerned with the properties and relationships of points, lines, angles, curves, surfaces, and solids. It implies the existence of objects in a continuous medium such as the circle in Figure 01. Such objects can be transformed into another level of abstraction with a formula. For example, the circle can be described by the formula:
x2 + y2 = 1, where x and y are the coordinates of a point P(x,y) on the circle of radius 1. This algebraic representation is very useful if we wish to study objects beyond our visualization such as something in 5-dimensional spacetime, or when the concept of continuous medium breaks down (as will be discussed presently for the case of quantum gravity).
|



 R2 R1.
R2 R1.


 x) = q(
x) = q( 0, dy/dx = (1+q)x, which equals to the usual form only when q = 1.
0, dy/dx = (1+q)x, which equals to the usual form only when q = 1.

 ---------- (1),
---------- (1), = 1.054x10-27 erg-sec is the Planck's constant divided by 2
= 1.054x10-27 erg-sec is the Planck's constant divided by 2
 ,
, 
 x ---------- (2),
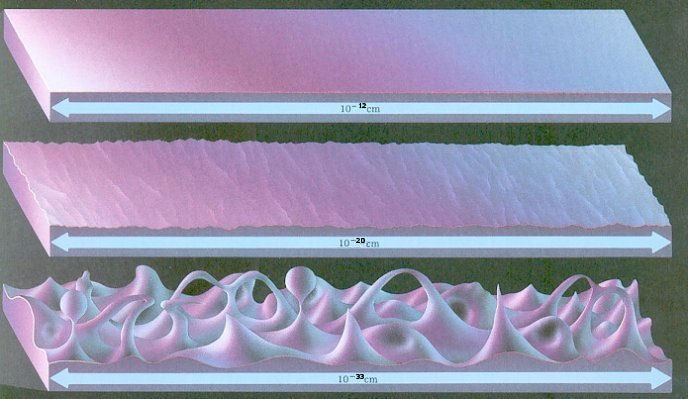
x ---------- (2), 1028 cm, i.e., about the size of the universe, the uncertainty becomes
1028 cm, i.e., about the size of the universe, the uncertainty becomes  , and 1/t to the frequency
, and 1/t to the frequency  to re-write (at gamma-ray frequency of ~ 1020 Hz) :
to re-write (at gamma-ray frequency of ~ 1020 Hz) :