Calabi-Yau Manifold

Calabi-Yau Manifold for Dummies :

Topology, Chern Class, Curvature, Riemann Surface and Complex Manifolds, Kahler Manifold, Calabi's Conjecture, Calabi-Yau Manifold

The concept of Calabi-Yau manifold can be best explained by defining the terminology, without which it is very difficult to comprehend.


• Topology - The formal definition involves language in "Set theory". Translating into plain English, it is the branch of

  mathematics that studies the properties of spatial objects from their inherent connectivity while ignoring the detailed form. The examples in Figure 04 shows that the 2-dimensional objects are separated into different class (space) according to the number of holes in them. Objects in each space have the same topology as long as they can be moulded into each other by deformation, twisting and stretching but no discontinuous operation such as cutting. Topology in higher dimension is more complicated than the 2-dimensional example, but the general idea remains the same. The classification of topological equivalent objects depends on the Euler characteristic = V - E + F, where (for 1 or 2 dimensional object) the number of vertices V = # of (n+1) or more edges meeting at a point + # of end points (n is the dimension of the object), the number of edges E = # of intersections of 2 faces or more + # of boundaries, and F is the number of faces. Table 01 shows some of the geometric objects

  Figure 04 Topology [view large image]

  together with the Euler characteristic. The objects with the same Euler characteristic belong to the same topological class even though they could look very different.

  
  

  Table 01 Euler Characteristic for some Geometric Objects

• Chern Class - Chern class is used to characterize the differences between two manifolds. If two manifolds have different Chern classes, they cannot be the same, but the converse is not always true: two manifolds can have the same Chern classes and still be different. The number of Chern classes depends on the number of complex dimensions (1 complex dimension implies 2 real dimensions) :
  

  1. For 1 complex dimensional manifold, there is just one Chern class, the first Chern class, which equals the Euler characteristic. In Figure 05, the complex 1-D sphere has 2 spots with zero net flow implying a first Chern class = Euler characteristic = 2, while the torus has no such spots and has first Chern class = Euler characteristic = 0. 2. The 2 complex dimensional manifold has a first and a second Chern class. The first one assigns an integer coefficients to subspaces (the 1-D manifold within the 2-D manifold), while the second one (the last one) always equals to the Euler characteristic. 3. The n complex dimensional manifold has a first and a second, ... nth Chern classes. The

  Figure 05 1-D Chern Classes [view large image]

  first one assigns an integer coefficients to subspaces (the 1-D manifold within the n-D manifold), while the second one assigns another number to subspaces (the 2-D manifold within the n-D manifold), ..., the last one always equals to the Euler characteristic.

  The first Chern class is vanishing (or zero) if all the tangent vectors on a manifold can be oriented to the same direction. This is impossible on a 2-D sphere, but can be done on the surface of a 2-D torus. Chern class is useful for learning the big picture of the manifold, to check out the number and types of sub-objects the manifold can hold. It is something similar to taxonomy, which classifies animals into species, genus, ..., kingdom. BTW, The Chern in Chern class is referred to Shiing-Shen Chern (, 1911 - 2004), who was a Chinese mathematician and the mentor of S. T. Yau.




Curvature - The curvature K of one dimensional object is determined by the formula : K = |d(dy/dx)/dx| / [1+(dy/dx)2]3/2 ---------- (1) while the square of an element of an arc on the curve is : ds2 = [1+(dy/dx)2] dx2 ---------- (2) The factor in front of dx2 is the 1 dimensional metric tensor g11 for a smooth manifold. An Euclidean example is a straight line described by the formula : y = ax + b ---------- (3) which produces K = 0, and ds2 = (1+a2) dx2. For a horizontal line such as the one shown in Figure 06, a = 0 and ds = dx. A circle provides an 1 dimensional non-Euclidean example, it is expressed by the formula : x2 + y2 = r2 ---------- (4) which yields K = 1/r ---------- (5),

Figure 06 Curvature of 1-D Object [view large image]

and ds2 = r2/(r2 - x2) dx2 ---------- (6). Note that there are two singularities at x = r. However, integration from x=-r to x=r returns a finite arc length of s = r.

Bypassing the mathematical formula as mentioned above, the curvature at a point P on a 1 dimensional curve can be defined as the reciprocal of the radius of the circle that best matches a curve at a given point (see insert in Figure 06). Viewing from top, curvature for a convex curve (like a circle) has negative sign, while the concave curve (like the bottom half of a cut-off circle) has positive sign.

Defining curvature for 2 dimensional object is more complicated because there are infinite number of curves that can pass through any point on the surface. Followings are some of the various definitions, which are related to the understanding of Calabi-Yau manifold :

1. Gaussian Curvature - The Gaussian curvature K is defined by multiplying the largest curvature k₁, and smallest curvature k₂ (i.e., K=k₁k₂) of the family of sectional curves perpendicular to the tangent plane at a given point as shown in Figure 07 at the saddle point of

the hyperbolic paraboloid surface. According to the Gauss-Bonnet Theorem the sum of the Gaussian curvatures over the whole surface equals to 2 multiplied the Euler characteristic 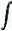, i.e. : A K dA = 2 ---------- (7) This theorem means that the overall curvature of the surface is fixed. Bending and pulling the surface may alter the curvature at every point, but these changes all cancel each other out. A trivial example is the surface of a sphere with unit radius (see insert in Figure 07). Its Gaussian curvature is 1 everywhere and

Figure 07 Curvature of 2-D Object [view large image]

the total surface area is 4. Thus = 2, which is the same as calculated previously by another method. See pseudosphere for an example of constant negative curvature.



2. Ricci Curvature - For higher dimensional manifolds (> 2-D), there are more than one tangent plane going through a point on the surface. The Ricci curvature is the average of the Gaussian curvatures associated with all these planes. Thus, a manifold can be Ricci flat (Ricci curvature = 0) without being flat overall. For the 2-D spherical manifold in Figure 07, the Ricci curvature equals to the Gaussian curvature since there is only one tangent plane. The Ricci curvature tensor R_ik appears in the 4 dimensional General Relativity Field Equation as :
R_ik - g_ikR/2 = 8GT_ik/c⁴ ---------- (8)

where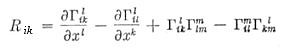

,

R = gikRik is the scalar curvature, gik is the metric tensor in the

square of the line element ds² = g_ikdxⁱdx^k (similar to the 1-D example in Eq.(6)) to be determined by the field equation (8),

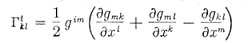is the Christoffel symbol, and Tik is the energy-momentum tensor, the indices

i, k, ... run from 0, ..., 3. Thus a Ricci flat curvature, i.e., R_ik = 0, is a solution to an empty universe for the field equation. Note that identical upper and lower indices stands for summation in N dimensions, e.g., xⁱy_i = x¹y₁ + x²y₂ + x³y₃ for N = 3.

3. Riemann Curvature - This is the curvature that completely determines the form of a manifold. It has 20 components (in 4 dimensions) splitting half into the Ricci tensor and the other half into the Weyl tensor. The Weyl tensor does not convey information on how the volume of the body changes, but rather only how the shape of the body is distorted by the tidal force or gravitational radiation. In dimensions 2 and 3 the Weyl curvature tensor vanishes identically. In dimensions 4, the Weyl curvature is generally nonzero.


• Riemann Surface and Complex Manifolds -

Riemann surface is manifold in complex number involving a pair of real and imaginary axes. Conformal mapping can be performed between Riemann and flat surfaces. This process may change the length scale but the angles between things are always maintained. Such property makes calculations easier than working on non-complex manifold. Riemann surfaces must be orientable meaning they have two sides like a beach ball, rather than just one side like a Mobius strip. In addition, they can be classified by their genus g (number of holes). The Euler characteristic = 2 - 2g. There are complex manifolds in higher dimensions with similar properties, but the different regions or patches of such manifold have to be properly attached in order to be qualified as complex.

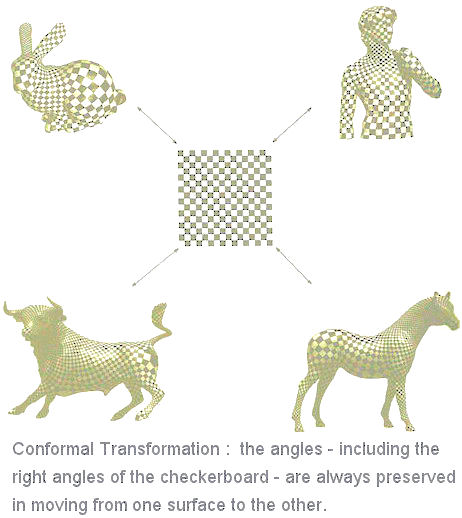Figure 08 Conformal Mapping [view large image]

• Kahler Manifold -
  1. It is a complex manifold.
  2. It is in between the Hermitian and flat manifolds in the sense that for a small displacement the metric g_ik varies as and 0 respectively, while the Kahler manifold changes as ². Such manifold has already many existing mathematical tools for its further study.
  

3. Parallel transport is a process of moving vectors or spinors along a path on a manifold that keeps the lengths as well as the angles between any two vectors unchanged (see Figure 09a for moving a vector on spherical surface by maintaining a southerly direction and tangential to the surface. if the direction changes at the end of a closed path, then there is curvature over the path). 4. Holonomy Group contains all the elements, which are closed paths formed by parallel transport, e.g., the path 1, 2, 3 in Figure 09.

Figure 09 Parallel Transport Symmetry [view large image]

5. For a Ricci flat manifold, a vector or spinor retains its orientation after moving through a closed path. Such spinor is called "covariantly constant spinor" and is a member of the SU(3) (3 complex or 6 real dimensions) holonomy group.

6. J operation is to rotate the vector by 90^o or multiply by i in case of complex dimension.
7. The Kahler manifold has the special property that it is symmetrical under the process of : J operation + parallel transport or vice versa, i.e., JW₁ = W₂ as shown in Figure 09b. This symmetry (known as internal symmetry) imposes another set of constraints on the mathematical formulation, drastically simplifying calculations.




Calabi's Conjecture - It was surmised that whether a certain kind of complex manifold - a space that is compact (finite in extent) and "Kahler" - could satisfy the general topological conditions of vanishing first Chern class and could also satisfy the geometrical condition of having a Ricci-flat metric (excluding the flat torus). Calabi-Yau Manifold - By expressing the conjecture in terms of nonlinear partial differential equations, S. T. Yau was able to prove the existence of many multi-dimensional shapes (now called Calabi-Yau manifolds) that are Ricci-flat, i.e., satisfying the Einstein equation in 3 complex dimensions and empty space, though the precise expressions for the metric tensor gik associated with such manifolds are still unknown. Figure 10 is a rendering

Figure 10 Calabi-Yau Manifold [view large image]

of the 2 dimensional cross-section from a 6 dimensional Calabi-Yau manifold.

The superstring theory has conformal invariance automatically built into it as the world sheet possesses conformal structure. Subsequent investigation shows that in order for a conformal field theory to survive the quantization (via the Feynman's prescription of summing over all the world sheet surfaces with weighting factors) the Calabi-Yau manifold should not be exactly Ricci-flat, but the deviation is not large enough to throw out its adoption to the superstring theory in its original form. Another new discovery is the mirror symmetry, which links two Calabi-Yau manifolds with opposite Euler characteristic (i.e., + and -) to the same conformal field theory (in a space one dimension lower). Such kind of duality always implies a simpler mathematical formulation in one of the alternatives.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu