 |
A group is defined as a collection of elements (a set), which are labelled a, b, c, ... and so on, and which are related to one another by the following rules:
- If a and b are both members of the group G, then their product, c = ab is also a member of the group G.
- The process is associative, i.e., a(bc) = (ab)c.
- There must be an element, called the unit element and usually denoted by I, defined so that
aI = a, bI = b, and so on for all elements in the group.
- Each element has an inverse, written as a-1, b-1 and so on, defined so that aa-1 = I and so on.
|
|
A group for which ab = ba is an Abelian group. The set of ordinary integer numbers ( ... -3, -2, -1, 0, 1, 2, 3, ...) under "addition" is a simple example of an Abelian group, where "0" is the unit element and the inverse is the same number with opposite sign. |

 = |g1
= |g1 gi|gj
gi|gj ij, where
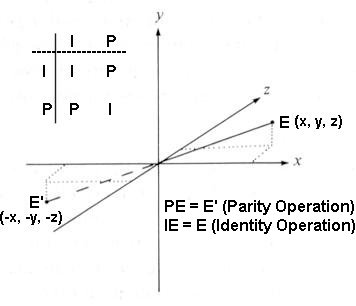
ij, where  j. Note that state vector is different from the spatial point E(x,y,z) acted upon by the partiy operation as shown in Figure 01a, which illustrates the geometrical configuration involved in the operation. Whereas, the state vector is an entity in a mathematical formulation such as the equation in quantum theory.
j. Note that state vector is different from the spatial point E(x,y,z) acted upon by the partiy operation as shown in Figure 01a, which illustrates the geometrical configuration involved in the operation. Whereas, the state vector is an entity in a mathematical formulation such as the equation in quantum theory. .
.  , while the original configuration is represented by 2 "+" signs (red) along the x-axis and 2 "*" symbols (blue) along the y-axis.
, while the original configuration is represented by 2 "+" signs (red) along the x-axis and 2 "*" symbols (blue) along the y-axis.
 ,
, 1. For p = +1, the normalized eigenvector is |P
1. For p = +1, the normalized eigenvector is |P which is symmetric; while for p = -1, the normalized eigenvector is |-P
which is symmetric; while for p = -1, the normalized eigenvector is |-P which is anti-symmetric.
which is anti-symmetric. ) ( 1 -1 ) so that
) ( 1 -1 ) so that  (x) and
(x) and  -x, then
-x, then  and K mesons. Spin-0 with positive parity such as the Higgs boson is called a scalar. A vector boson (photon) has spin-1 and negative parity, while a pseudovector boson has positive parity.
and K mesons. Spin-0 with positive parity such as the Higgs boson is called a scalar. A vector boson (photon) has spin-1 and negative parity, while a pseudovector boson has positive parity. , p(before) = +1 which is not equal to p(after) = (+1)(+1)(-1) = -1.
, p(before) = +1 which is not equal to p(after) = (+1)(+1)(-1) = -1. kbk|a, k
kbk|a, k , where
, where 
 )ij = (D*)ji. Thus, for the matrix D(P) in the above example, D
)ij = (D*)ji. Thus, for the matrix D(P) in the above example, D

 respectively. Note that each subspace contains its own state vector (an one dimensional vector in this simple example); there is no mixing or crossover.
respectively. Note that each subspace contains its own state vector (an one dimensional vector in this simple example); there is no mixing or crossover. D2 by multiplying the two smaller representations, i.e.,
D2 by multiplying the two smaller representations, i.e.,  .
.
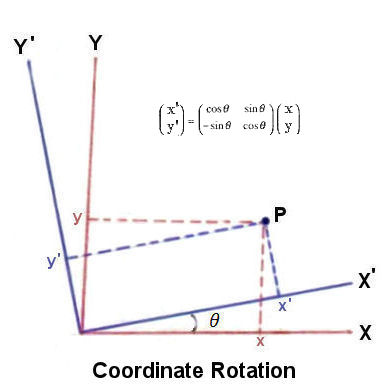
 )] x + [sin(
)] x + [sin( ----- (1c)
----- (1c)