
His bold step is to declare that the concept of entropy is also applicable to other thermodynamics processes such as those shown in (a) and (b) although no heat transfer is discerned. It has the peculiar property that it always tends to increase in a closed system. As many other thermodynamics entities, it is well defined only in a system at equilibrium. It is a function of the independent variables V (volume), T (temperature), P (pressure); but V, E (energy), N (number of particles) are more useful in connection with the information theory to be discussed presently.


 10-16 erg/K, which is very small comparing to the entropy generated in raising 1 gram of water by 1oC at room temperature (27oC), i.e.,
10-16 erg/K, which is very small comparing to the entropy generated in raising 1 gram of water by 1oC at room temperature (27oC), i.e.,  S = 1.4x10-8 erg/K.
S = 1.4x10-8 erg/K.
 (pi) log2(pi), where pi is the probability of finding the particle in location xi or velocity vi in a box of volume V, and SMI is always a positive defined quantity. This is not entropy as both Shannon and John von Neumann would have it. Instead thermodynamics entropy can be derived from SMI as shown in the followings.
(pi) log2(pi), where pi is the probability of finding the particle in location xi or velocity vi in a box of volume V, and SMI is always a positive defined quantity. This is not entropy as both Shannon and John von Neumann would have it. Instead thermodynamics entropy can be derived from SMI as shown in the followings.

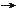 2V
2V

