Statistics, Chance, and Probability Distribution

Contents

Statistics and Correlation

Statistics can be considered as experimental or observational mathematics. It uses the collected data to derive an estimated value of a parameter such as population mean, averaged temperature, ... etc. These values would not be very precise, but could present a vague idea in the absence of elaborate measurements, hence it is often associated with chance or probability. Many methods were invented over the years to check out the statistical significance of a given set(s) of data. Unfortunately, the data are often manipulated to suit some purposes, hence the saying : "There are three kinds of lies: lies, damned lies, and statistics".

Figure 01 House Survey [view large image]

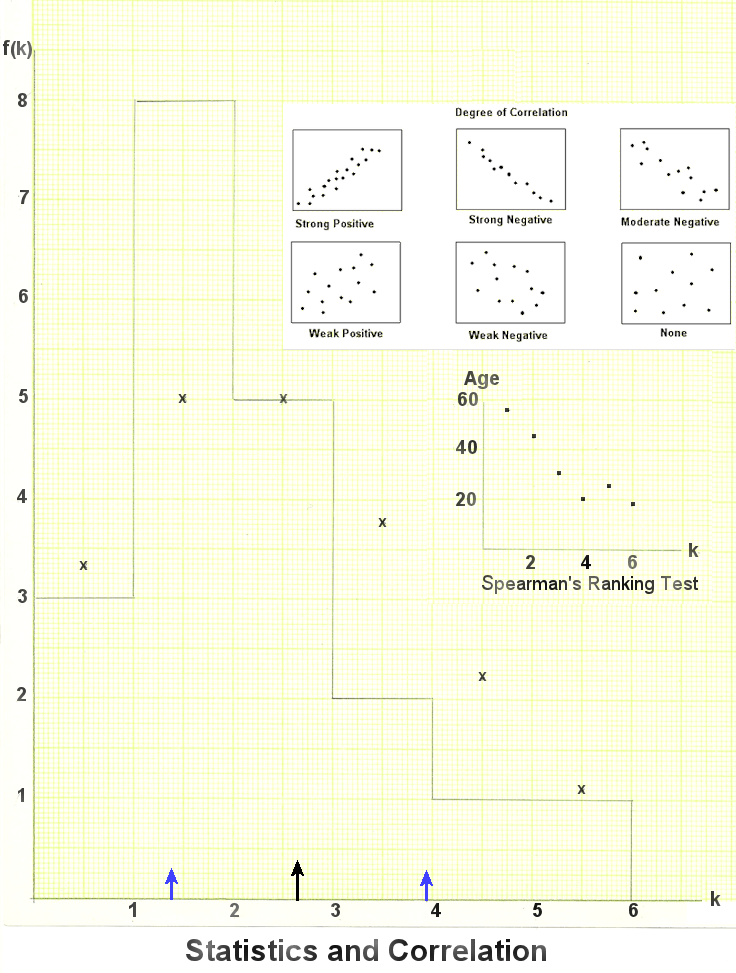
The following example illustrates the most elementary statistics about the number of occupants k in each of the N=20 houses on a street (Figure 01), f(k) denotes the frequency of occurrence hence f(k)/N is the probability of finding k occupants among these houses. It is often referred to as the Probability Distribution (note that its total is normalized to 1). Table 01 below contains the data collected in a survey.

Table 01 Number of Occupants in each House on a Street

Figure 02 Statistical Graph [view large image]	From these statistical evaluations, we obtain a vague idea about the occupants on this street. However, many details such as gender, occupation, age, ... are missing. To obtain a little bit more information, the survey could include the averaged age of the occupants in each category as shown in the 5th column of Table 01.

Table 02 Spearman's Ranking Test

Chance (Probability) and Information

Permutation - Since all 5 of the contestants has a chance to receive the bronze crown, after which the silver goes to the remaining 4, lastly each 3 of them has a chance for the golden one, the total number of possible arrangements is 5P3 = 5 x 4 x 3 = 60. In general the number of possible sequences of k objects from a collection of n is : nPk = n x (n-1) x (n-2) ... (n-k+1) = n!/(n-k)! = N (the number of different arrangements)

Figure 03a Permutation and Combination

where n! = n x (n-1) x (n-2) ... 1 is the factorial of n and 0! = 1 (negative number is forbidden).

The probability for a particular winning lineup (e.g., bronze to B, silver to A, gold to D) is just the reciprocal of the number of arrangements, i.e., P(5,3) = 1/60. This choice conveys a message or information about the selection of that year's winning contestants. The information can be quantified as I = - log2(N) - 6 bits in the example. In the very unusual case where the winner of the crown can return to the pool to be judged again for the next crown, the number of contestants is always 5. Therefore the number of arrangements is 5 x 5 x 5 = 53 = 125. Thus nPk = nk in general for such case (see a less colorful example in Figure 03b).

Figure 03b Permutation Example

	Combination - Suppose another weird beauty contest awards 3 gold crowns to the 3 winning contestants, therefore the ordering really doesn't matter. The number of arrangements is reduced by a factor of 3 x 2 x 1 = 6 in the example and is denoted by 5C3 = 60/6 = 10 (Figure 03c). The general formula for such case with no selection preference is : nCk = = n!/[k!(n-k)!].
Figure 03c Combination Example

	Examples : For N = 60 : by taking n = 5, then I = - 5 - 3.32 x log10(60 / 32) = - 5 - 0.9 = -5.9 . For N = 13983816 : by taking n = 23, then I = -23 - 3.32 x log10(13983816 / 8388608) = - 23.737.
Table 02a 2n to Decimal

Probability Distribution

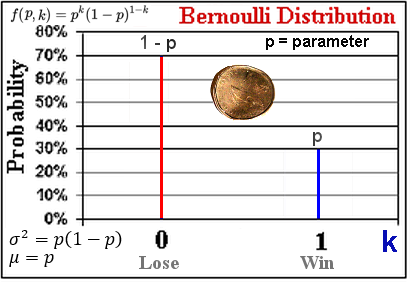		As shown in Figure 05, since the events are always simultaneously opposite to each other the distribution is symmetrical about the mid-point. When the Binomial coefficients are normalized by dividing the sum of all the 's, which is just 2n, they becomes the probabilities. The Bernoulli distribution is the special case of (a + b)n with n = 1 (k = 0, 1) showing both events occur once at the same time. The discrete Binomial distribution can be approximated by the continuous Normal distribution (aka the Bell curve) with k x :
Figure 04 Bernoulli Distribution [view large image]	Figure 05 Binomial Distribution [view large image]	. For the case of n = 6, p = 0.5: = 3, = 1.2247, f(3) = 0.3258 (see Figure 05).

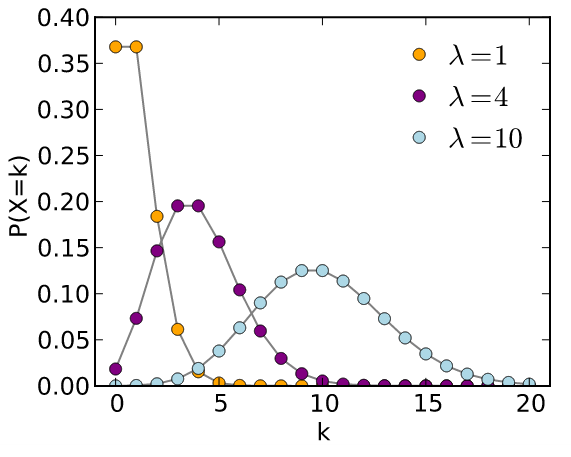	The Poisson distribution is used for estimating random occurring phenomenon based on a more likely one. The formula is : where is called the "intensity", which is usually associated with the more frequent occurrence. In the example of occupants number, = 3 (at k = 3) seems to fit better. The result is plotted with crosses (x's) in
Figure 06 Poisson Distribution [view large image]	Figure 2 (by scaling with a multiplication factor of 22.22). Figure 06 shows that the Poisson Distribution approaches the Normal Distribution as 10

		Quantum physics depends extensively on the probability distribution of small particles to understand the nature of microscopic objects. A very simple example is about a particle inside a box, which is represented by an infinite square well. The probability distribution is in the form of P(x) = sin2(nx), where n is an integer specifying the state of the system, which is associated with the energy level in this case. A few of the probability distribution are shown in Figure 07. Another exactly solvable case for the Schrodinger's equation is the Hydrogen atom. The probability distribution is related to the electron (probability) density around the nucleus - the proton. A few of the states are displayed in Figure 08 for its radial distribution. These states are also
Figure 07 Infinite Square Well Probability [view large image]	Figure 08 H Atom Distribution [view large image]	related to the energy level, but there are more complicated configuration involving orbital angular momentum, spin, ... Some of such states are

Confidence Interval

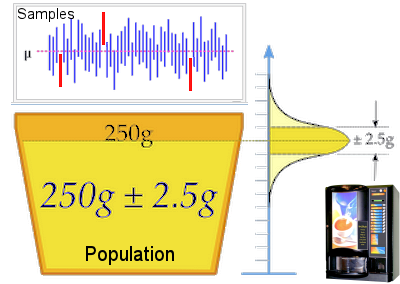A confidence interval (CI) is the interval for sets of measurements, which are likely to including the unknown parameter, e.g., the mean of the population sample to be verified (see top portray in Figure 09). The technique requires a knowledge of the population standard deviation as shown in the following example. A coffee vending machine customer decides to check out the manufacturer's specification, which claims to dispense 250 g (the ) of the liquid with a margin of error to be 2.5 g (the as shown in Figure 09). The procedure to determine if the machine is adequately calibrated, is to weigh n = 25 cups of the stuff, i.e., x1, x2 ... x25, and to perform the following calculation. Data from both the manufacturer (taken to be the

Figure 09 Confidence Interval [view large image]

whole population) and the customer's sample are considered to follow the pattern of normal distribution. Sample data gathering in this case has 50 sets of 25 cups each as shown in the top portray in Figure 09.

Normal Probability Table [view large image]	This example shows that the estimate of becomes more accurate as the CI getting narrower. This objective can be achieved with increasing n, i.e., by collecting more data in the sampling. However, it implies more work, which is especially more difficult in the old day when calculation was not computerized.

The confidence level is used for the search of the Higgs particle by scientists in LHC. They first calculate all the possible events excluding those related to the Higgs' from the Standard Model. This is the /SM = 1 straight line in Figure 10 (don't confuse it with the standard deviation). Then the probability /SM for similar Higgs-looking background events are estimated and plotted by the yellow and green bands with 95% CL with the

Figure 10 CL in Higgs Discovery [view large image]

mean (dark dotted curve) in Figure 10. The occurrence of rare events outside the expected boundary indicates additional contribution by the Higgs particles, the the corresponding energy (~ 125 Gev) is the mass of the Higgs particle. The ultimate goal is to obtain a signal at 99% CL.

Chi Square Test

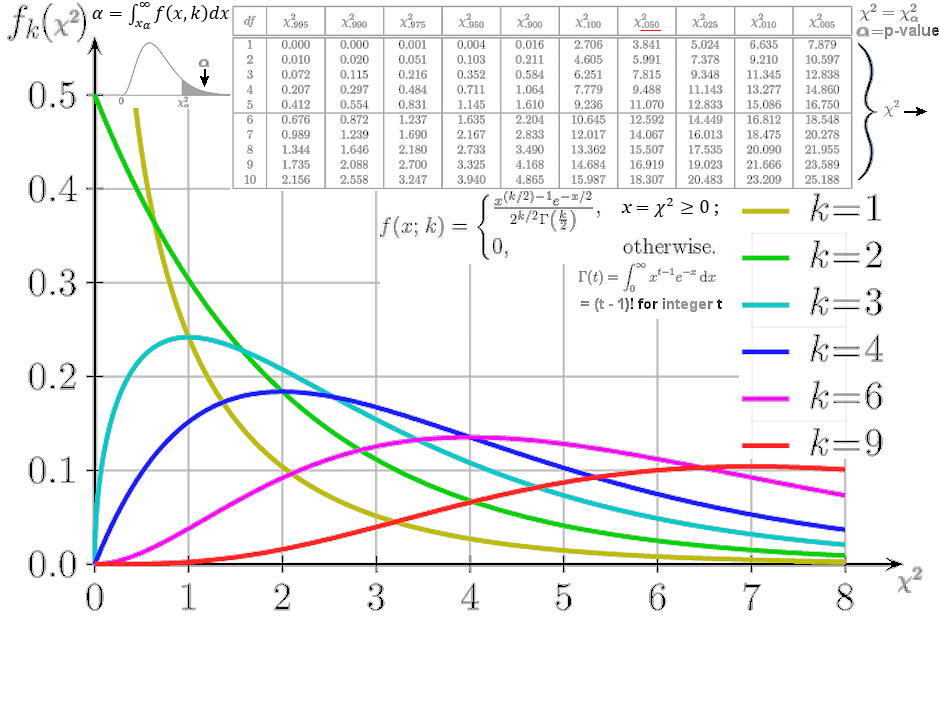The Chi Square Test is a tool to check out if the measurements relate to a hypothesis is true or not. It was originally intended to judge if the statistical data are significant. It doesn't even come up with a degree of correlation as provided by the Spearman's test. However, it becomes a gold standard for evaluating statistical data over the years since its invention in the 1920's. There is a 2014 article in Nature to remind everyone to use it carefully. A table of 2 and graphs of f(2) for different k is shown in Figure 11a. The subscript in 2 on the top row is the % probability beyond 2 as shown by the dark shade inside the curve at top left. Usually, denotes the probability that the null hypothesis (the measurements are related to the

Figure 11a Chi Square Distribution

assertion) is right. Thus a small nummber for indicates that the null hypothesis is probably wrong. The boundary is set at 2=0.05. The p-value = = 0.05 is arbitrarily chosen but accepted by most researchers. A value of 2 to its left (smaller , larger ) means support for the hypothesis, and otherwise to the right.

By definition x = 2 is calculated from , which is not easy to solve even numerically. Fortunately, "Stat Trek" has provided an online Chi-square calculator to facilitate the difficult task (click Figure 11b). The CV in there denotes the x, while P(X2 CV) denotes the percentage probability for the integration limits from 0 to x producing (1 - ). It is available for different values of k up to k = 50.

Figure 11b Online Chi2 Calculation

For the novice, it is important to distinct the difference between 2 (or x, the independent variable) and the (or p-value, the sum of probability). Also notice that increasing 2 always goes together with decreasing .

The Chi-square distribution according to different degree of freedom is tailored to the size of the collecting dataset from small sample size to set of large random numbers. The degree of freedom (df and denoted by k here) is essentially the number of data minus the number of constraints in compiling the statistics. For example, in calculating the standard deviation s with n data points, the degree of freedom is n - 1 because one of the data cannot be arbitrary, it is constrained by the relation (for a known value of ). Another example illustrates 2 variables linked by the formula x + y = 10, or x = 10 - y, it is clear then that only y can be varied arbitrarily, x is constrained by the formula. Thus, the degree of freedom is 1 in this case.

Figure 11c Chi-Square df4 Distribution Function

BTW, it doesn't matter whether to use n or (n - 1) for n >> 1.

• The mean of the distribution is equal to the number of degrees of freedom : = k.


• The variance is equal twice the number of degrees of freedom : ² = 2k.


• The maximum of f(x), i.e., f_max is obtained from df(x)/dx = 0 giving x_max = k - 2 (for k 2). See Figure 11c for a pictorial illustration with the k = 4 Chi-square distribution curve (in red).


• For large k, x_max ~ ; the Chi-squre distribution approaches the normal distribution. By substituting x = - x' and then x = + x' (with k x' 0) to f(x), it reveals f(x) (1 - x'²/4) for both substitutions proofing that f(x) is symmetrical about the mean .


• The ²_0.05 is chosen such that ²_0.05 > + = k + (2k)^1/2 for all k's. In particular, for large k and with minor adjustment (to the usage of the Normal Probability Table) an approximate expression can be derived : ²_0.05 = k + 1.78 (2k)^1/2. It yields good agreement with the online calculation giving 67.8 (vs 67.5) for k = 50; and 18.0 vs 18.3 for k = 10.

There are two types of Chi Square test involving different kind of data as shown in the following examples :



Category Test for Independence - This type collects data by asking qualitative questions such as names or labels. A contingency table is compiled by counting the number of responses in each category (Figure 12). This example is about an election survey to check out if voter gender is related to voting preference (for political parties A, B, and C). The null hypothesis in this case is for no preference. Since there are Nr = 2 rows and Nc = 3 columns the degrees of freedom df = (Nr-1)(Nc-1) = 2.

Figure 12 Contingency Table [view large image]

There is always one degree of freedom less because of the restriction imposed by the sum.

	The expected frequencies are computed by the formula Er,c = (nr x nc)/n, where nr, nc are the row and column totals, n is the grand total number in the survey. The Er,c's have the effect of blurring the distinction between the political parties and genders and so represent the
Figure 13 Frequency Table [view large image]	null hypothesis. Or,c's are the raw data from the survey as shown within the red line boundary in Figure 12. These data are collectively shown in the frequency table in Figure 13.

From these data, a value is then computed to yield ² = 0.176 . According to the table in Figure 11a for df = 2, it produces a p-value much greater than the 0.05 level. It is thus concluded that the probability (p-value) is high enough to sustain the null hypothesis, i.e., there is no correlation between genders and voting preferences. This kind of statistical evaluation is valid only if (a) the sample is random, (b) the population is at least 10 times as large as the sample, (c) the frequency count is at least 5, (d) the variable under study are each categorical.



Numerical Fitness Test - This type of test compares observation with theoretical prediction. In this example, a gambler wants to check out if the three dice game in a casino (Figure 14) is fair by recording the frequency of sixes in 100 rolls (see Table 03 below). The theoretical data are derived from the Binomial Distribution with n = 4. Thus the Binomial coefficients are 1, 3, 3, 1 and b = p = 1/6, a = 1 - p = 5/6. The expected counts are just the terms in the Binomial expansion multiplying by 100 (the number of test). The final computation yields 2 = 2.27. For df = 4 - 1 = 3, the Chi Square Table in Figure 11a indicates a p-value between 0.9 and 0.1, i.e., greater than the 0.05 significance level. The gambler proceeds to play with re-gained trust.

Figure 14 Three Dice Gambling [view large image]

The formula is : where Oi is the observed frequency, Ei the expected frequency as asserted by the null hypothesis, and n the number of cells to be evaluated. For perfect match, Oi = Ei, 2 = 0, = 1.




# of Sixes	Observed Counts Oi	Expected Counts Ei
0	64	1(5/6)(5/6)(5/6)x100 = 58
1	30	3(5/6)(5/6)(1/6)x100 = 34.5
2	5	3(5/6)(1/6)(1/6)x100 = 7
3	1	1(1/6)(1/6)(1/6)x100 = 0.5

Table 03 Three Dice Game Evaluation

Lastly, let us consider three specific cases :


1. For the case when all observations agree with expectations, i.e., O_i = E_i for all i. It follows that ² = 0 << ²_0.05. The null hypothesis is 100% correct.
2. Now consider the case when all O_i = 3 E_i (a case with obvious discrepancy). Therefore, ² ~ 4k > ²_0.05 according to the estimated value of ²_0.05. Thus, the null hypothesis can certainly be rejected.
3. However, when all O_i = 2 E_i, we would have ² ~ k < ²_0.05 implying the rejection of the null hypothesis is not solid.

According to the article in Nature (as mentioned earlier), the problem of relying on the p-value is in the underlying hypothesis, which challenges the null hypothesis. As shown in Figure 15, the more outlandish the hypothesis the more chance it would fail even at the 0.01 level. In other words, the significance p-value varies with the nature of the hypothesis, 0.05 is not the absolute standard as most researchers assumed. A subjective element about the likelihood of the hypothesis is thus introduced into the process. On top of such fallacy, there are cases when data

Figure 15 Statistical Errors [view large image]

are massaged to yield a low p-value. It is suggested that claims of p-value around 0.05 often involves fishing for significance; failure to replicate results is another sign; p-hacking (manipulation of data) can also be detected by looking at the method of analysis often banished to the discussion section at the end of the paper.

Statistical Mechanics

(Maxwell-Boltzmann, Bose-Einstein, Fermi-Dirac)

Maxwell-Boltzmann Distribution

Boltzmann in 1868. The atomic composition of gas was not widely accepted by physicists at that time, and nothing was known about atomic structure; thus, the micro-state was invented to accommodate the particles with population Ni in an energy state Ei, which contains a number of cells gi (corresponding to different orientations for example). These micro-ensembles are supposed to link with the macroscopic variables such as the total number of particles N = Ni, the total energy E = NiEi, the volume of the system V, temperature T, ... The probability of the ith occurrence would be Ni/N, the distribution (against energy or velocity) of which was derived by Maxwell-Boltzmann under certain assumptions :

Figure 16 Maxwell-Boltzmann Distribution [view large image]

• The formula is derived for a system of ideal gas where the particles move freely inside a stationary container of volume V without interacting with one another, except briefly in elastic collisions. This system of particles is assumed to have reached thermodynamic equilibrium. This assumption is applicable for a system of rarefied gases at ordinary temperatures since the effect of inter-molecular interaction is minimized in such condition.


• The micro-states are specified by energy levels. There are sub-divisions called cells within each level. Particles in these cells would have some special features to distinct themselves (e.g., different orientations) but having the same energy. It is called degeneracy in modern physics. The micro-states are assumed to be discrete as illustrated in Figure 16, in which only 2 cells per energy level is depicted for illustrative purpose. There could be a lot more, and may not be the same number in each energy level. In going over to continuous distribution, e.g., against the velocity v, the summation would be converted to integration.


• The particles are identical but distinguishable by assuming that the trajectory of the particles can be traced (at least in principle).


• There is no restriction on the number of particles with energy E_i and within its corresponding cells (degenerate states).

The following derivation starts with a discrete system and then converts to continuous velocity distribution (see Figure 16 for pictorial illustration). Here's the mathematics in 4 steps :

(1) Statistics - The number of ways to select one particle among N into the E_a micro-state is just N, N(N-1) for selecting two, N(N-1)(N-2) for selecting three, and so on ... with the first one to be the highest order, the second one the next, ... This is just the permutation for selecting "a" entries among N objects with ordering, i.e., P(N,a) = N(N-1)(N-2)...(N-N_a+1) = N!/(N-N_a)!. The amount is reduce by a factor of N_a! if ordering is ignored; this is called combination C(N,a) = N!/[N_a!(N-N_a)!] (see Figure 16). Accordingly, for a set of levels labeled by a, b, c, ... k, and by filling them one after the others, ignoring ordering, the number of ways W is :

For example, with g = 3, n = 2 (represented by A and B), gⁿ = 3² = 9 as illustrated below :

(2) Most Probable Configuration - At equilibrium, the distribution would be in a most probable configuration. Mathematically, it involves maximizing W by a special arrangement of N_i at various levels. However, this special configuration has to be consistent with the constraints N = N_i and E = N_iE_i. The method of "Lagrange Multipliers" is used to perform such kind of maximization. Essentially, if the constraint for f(x) is in the form h(x) = 0, then the maximizing should be performed on L(x,) = f(x) + h(x), where is a constant (the Lagrange multiplier) to be determined. In the current derivation, it is easier to deal with ln(W) in the following maximizing scheme :


(3) Macroscopic Link - A macroscopic formula emerges by substituting the optimized value of N_i into ln(W) :
ln(W) = ( + 1)N + E.
An infinitesimal change in energy at constant number of particles would induce a small adjustment of the configuration : d[ln(W)] = dE. Since the Boltzmann's definition of entropy is S = k ln(W), thus dS/k = dE, where the Boltzmann constant k = 1.38x10^-16 erg/K.

In thermodynamics, the infinitesimal change in energy is related to the other macroscopic variables by the identity : dE = TdS - pdV + dN, where T is the temperature, p the pressure, and the chemical potential related to the change of chemical energy G with the change in the number of ith species Ni, i.e., = dG/dNi (Figure 17). Since both the volume V and number of particles N are unchanged in the Maxwell-Boltzmann statistics, dE = TdS. By comparing the formula derived from the microscopic consideration, i.e., dE = dS/(k), the Lagrange multiplier can be identified as = 1/kT.

Figure 17 Chemical Potential [view large image]

(4) Distribution in Velocity - Since the collisions between particles are elastic in the Maxwell-Boltzmann statistics, the energy consists only kinetic energy, i.e, E_i = mv_i²/2. The variable range is now continuous, in particular the number of cells is given by g(v) = 4v² with each direction of the velocity represents a different cell (Figure 16). The probability of finding the particles with velocity v is :
    

Figure 18 Maxwell-Boltzmann Distribution
[view large image]

(5) Applications - In a simplistic model of heat capacity for metals, the constituent atoms are treated as harmonic oscillators (with no interaction between each others). The one-dimensional motion of such oscillator has energy E = mv²/2 + Kx²/2, and g_i = 1. According to the Maxwell-Boltzmann distribution, the averaged energy is :

See "Specific Heats of Solids and Phonons" for more information about the subject.

Designating v to be the average velocity, L the length of the tube, A the area at the ends, the change of momentum p in a round-trip starting from one end is p = p - (-p) = 2p = 2mv in a time interval t = 2L/v. By definition, the pressure P = F/A = N(p/t)/A = Nmv²/V or v² = PV/Nm, where F is the collective force from N particles and the volume V = LA. Using the relationship between v and T, we obtain the Gas Law PV = nRT, where n = 3N/N_A is the number of mole for 3N particles, R = kN_A = 8.314 J/mole-K the Gas constant.

Bose-Einstein Distribution

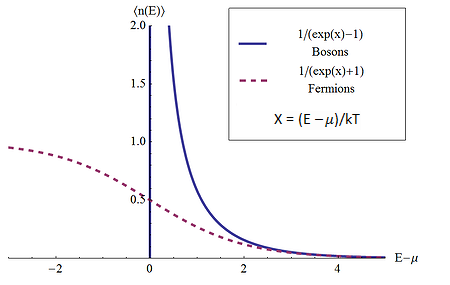		In deriving the Bose-Einstein distribution, it is assumed that the constituent gas particles are non-interacting at thermodynamic equilibrium and indistinguishable. There is no restriction on the number of particles in any quantum states. They are called boson, all of them have integer spin. Those are photon gas in the cavity of blackbody radiation, the coupled electron pair (Cooper pair) in superconductivity, and Helium-4 in Superfluidity.
Figure 19 BE-MB Distribution	Figure 20 BE-FD Distribution [view large image]	The methodology to derive the statistical distribution is similar to the treatment in the last section. The difference is on counting the occupation number.

The following derivation starts with the determination of the number of ways in which N_i indistinguishable particles can be distributed in g_i cells having same energy E_i.

(1) Statistics - The counting obviously involves the number of particle N_i. However, the re-arrangement of the partitions (the walls separating the cells and hence there are g_i - 1 of them) can also create different configuration. Thus, there are (N_i + g_i - 1)! possible permutations. Since the particles are indistinguishable, N_i! and (g_i - 1)! of the permutations are irrelevant. Therefore, the actual number of ways for each level is (N_i + g_i - 1)! / [N_i! (g_i - 1)!], and the probability W of the entire distribution of N particles is the product :

W = (N_i + g_i - 1)! / [N_i! (g_i - 1)!]

For example, with g_i = 3, N_i = 2, the number of permutations would be 4!/(2!2!) = 6 as illustrated below :
;
for g_i = 1, the number of ways at that level would be just one as shown :

(2) Comparison with the Maxwell-Boltzmann Distribution : Using the other form of the Stirling's approximation n! ~ nⁿe^-n

W ~ (N_i + g_i)^N_i+g_i/[(N_i)^N_i(g_i)^g_i] ~ g_i^N_i/N_i!

The final form is obtained by assuming g_i >> N_i >> 1, and (1 + N_i/g_i)^g_i ~ e^N_i. This is the condition for close match between the Bose-Einstein and Maxwell-Boltzmann statistics (Figure 19), and shows that the ideal gas is not really composed of distinguishable particles. Unlike the marked difference with the Fermi-Dirac statistics (Figure 20), they are very similar except when T ~ 0 K with most particles occupying the lowest energy level (g_i = 1 << N_i) forming the Bose-Einstein Condensate (BEC).

(3) Most Probable Configuration - The procedure is the same in the last section, except the mathematical details. The function to be maximized (with ln(W), Stirling's approximation, and Lagrange multipliers) is now (assuming g_i >> 1) :


(4) Macroscopic Link - A macroscopic formula emerges by substituting the optimized value of N_i into ln(W) :
ln(W) = N + E. An infinitesimal change in energy and number of particles would induce a small adjustment of the configuration :
d[ln(W)] = dS/k = dN + dE.
In thermodynamics, the infinitesimal change in energy is related to the other macroscopic variables by the identity :
dE = TdS - pdV + dN,
where T is the temperature, p the pressure, and the chemical potential related to the change of chemical energy G with the change in the number of i^th species N_i, i.e., = dG/dN_i (Figure 17). Since the volume V is constant, dE = TdS + dN. By comparing the formula derived from the microscopic consideration, i.e., dE = dS/(k) - (/)dN, the Lagrange multipliers can be identified as = 1/kT, and = -/kT , and N_i = g_i / [e^{(E_i - )/kT} - 1] .

		(5) Photon Gas in Cavity - Photon gas is the quantum version of electromagnetic wave when the particle-like behavior is dual to the wave property. It's main difference from the ideal gas is the way in reaching equilibrium. Whereas that state is attained by collisions in the latter case and the number of particle is conserved, the photon gas arrived at equilibrium by interacting with the matter in the cavity wall (Figure 21). The number of photons in a given state is not constant in the absorption and emission processes. However, the total energy remains the same at equilibrium, i.e., the total negative change of the chemical potential is balanced by the positive change.
Figure 21 Photon Gas [view large image]	Figure 22 Blackbody Radiation [view large image]	Consequently, the overall change is zero which implies the chemical potential = 0 or e-/kT = 1.

Derivation of the number of cells g_i is similar to the case of velocity distribution in Maxwell-Boltzmann statistics except that the counting is in the phase space Vx2x4p²dp where V is the volume of the cavity, p is the momentum of the photon (with energy h = pc), and the factor of 2 is for the 2 different polarization states. The Planck's constant h = 6.625x10^-27 erg-sec from the uncertainty relation px ~ h in quantum theory is conveniently taken as the basic unit (minimum size) of the microscopic states. Thus g_i = (V/h³)8p²dp.


Temperature at the upper layer of the Sun's photosphere is about 6000 K corresponding to _max ~ 480 nm (Figure 22), which is in the middle of the visible range and absorbed by plants to perform photosynthesis in the first step of the food chain.

Fermi-Dirac Distribution

(2) Most Probable Configuration - The procedure is the same in the last two sections, except the mathematical details. The function to be maximized (with ln(W), Stirling's approximation, and Lagrange multipliers) is :

(3) Macroscopic Link - A macroscopic formula emerges by assuming e^+E_i >> 1 (i.e., when the particles behave like ideal gas, see Maxwell-Boltzmann statistics) and substituting the optimized value of N_i into ln(W) :
ln(W) = N + E. An infinitesimal change in energy and number of particles would induce a small adjustment of the configuration :
d[ln(W)] = dS/k = dN + dE.
In thermodynamics, the infinitesimal change in energy is related to the other macroscopic variables by the identity :
dE = TdS - pdV + dN,
where T is the temperature, p the pressure, and the chemical potential related to the change of chemical energy G with the change in the number of i^th species N_i, i.e., = dG/dN_i (Figure 17). Since the volume V is constant, dE = TdS + dN. By comparing the formula derived from the microscopic consideration, i.e., dE = dS/(k) - (/)dN, the Lagrange multipliers can be identified as = 1/kT, and = -/kT , and N_i = g_i / [e^{(E - )/kT} + 1], or in the form of the continuous occupation index (probability for occupation of each cell at energy E) f(E) = N(E)/g(E) = 1 / [e^{(E_i - )/kT} + 1].
As shown in Figure 23, it has a peculiar property at T = 0 K, such that f(E) = 1 for E < (fully occupied), and f(E) = 0 for E > (none occupied). For finite temperature, more levels would be populated as T increases for E > , while the opposite trend happens for E < . The chance is always 1/2 at E = (see Figure 23). It will be shown presently that depends on the number density N/V. It is better known as Fermi Energy E_F .

(4) Free Electron Gas in Metal - To a good approximation, the valence electron can be considered as free from its bounds with the atomic nucleus. These electrons are treated as ideal gas in a box (Figure 23). The inter-electron and nucleus-electron interactions are neglected (with some justifications). The model has been applied successfully to the calculations of structures of degenerate stars, formulation of the Band Theory, electron emission from metallic surface including the photoelectric effect, electrical and thermal conductivity (Figure 24).

Derivation of the number of cells gi is similar to the case of Bose-Einstein statistics counting in phase space: Vx2x4p2dp where V is the volume of the cavity, p is the momentum of the electron, and the factor of 2 is for the 2 different spin states. The Planck's constant h = 6.625x10-27 erg-sec from the uncertainty relation px ~ h in quantum theory is conveniently taken as the basic unit (minimum size) of the microscopic states. Thus gi = (V/h3)8p2dp.

Figure 23 Fermi-Dirac Statistics [view large image]

In terms of energy E = p2/2m, g(E) dE = [(8Vm3/2E1/2)/h3] dE .

If a particular metal sample contains N free electrons, E_F can be calculated by filling up its energy states from E = 0 to E = E_F by definition. Hence

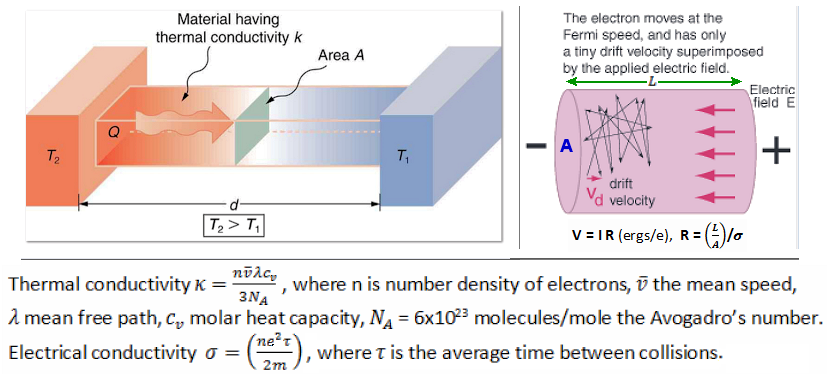Table 04 lists the electrical and thermal conductivity for some metals in descending sequence of EF. Theoretical calculations show that these conductivities are proportional to the electron number density (Figure 24). The table reveals that while some entries follow the trend, the others (the latter half) do not seem to conform. The deviation can be explained by interaction with phonons (coherent wave motion of the lattice), which determines the conductivity for some metals.

Figure 24 Conductivity by Electron Gas

Metal	Fermi Energy, EF (ev)	# Density (1028/m3)	Electric Conductivity (107/ohm-m)	Thermal Conductivity (w/m-K)
Aluminium (Al)	11.7	18.1	3.50	205.0
Iron (Fe)	11.1	17.0	1.00	79.5
Lead (Pb)	9.47	13.2	0.455	34.7
Copper (Cu)	7.0	8.47	5.96	385.0
Silver (Ag)	5.49	5.86	6.30	406.0
Sodium (Na)	3.24	2.40	2.22	134.0

Table 04 Electrical and Thermal Conductivity in Metal

(5) Application - The major application is in the "Band Theory of Metal".