Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Relativity, Cosmology, and Time

Hawking Radiation

    According to Stephen Hawking (1942 - 2018) himself, an inspiration came to him before going to bed one evening in 1970 (getting into bed is a rather slow process with his disability). He suddenly realized that since nothing can escape from a black hole, the area of the event horizon might stay the same or increase with time but it could never decrease. In fact, the area would increase whenever matter or radiation fell into the black hole. This non-decreasing behavior of a black hole's area was very reminiscent to that of entropy, which measures the degree of disorder in a system. One can create order out of disorder, but that requires expenditure of effort or energy such that there is an overall increase in disorder. In simple mathematical terms these statements can be expressed in differential forms as outlined below:

  1. From the definition of the Schwarzschild radius R = 2Gm/c2, and its surface area A = 4R2, we can derive an expression for the small change of the area dA by throwing in a small amount of mass dm:
    dA = (32G2/c4)mdm ---------- (16a).
  2. From E = mc2, Eq.(16a) can be rewritten to:
    dE = (c4/32mG2)dA.
  3. By definition, the corresponding increase in entropy is:
    dS = dE/T = (c4/32mTG2)dA ---------- (16b),
    where T is the temperature of the black hole in oK. But it has been shown in the topic of Black Hole Entropy that in term of Planck area:
    dS kB(c3/G)(dA/4) ---------- (16c).
  4. Equating Eqs.(16b) and (16c), we obtain a formula relating the mass m and temperature T for a black hole:
    T = hc3/(162GkBm) ---------- (16d).
This equation implies that the black hole is associated with a temperature T, and should emit radiation as any hot body. Thus, the black
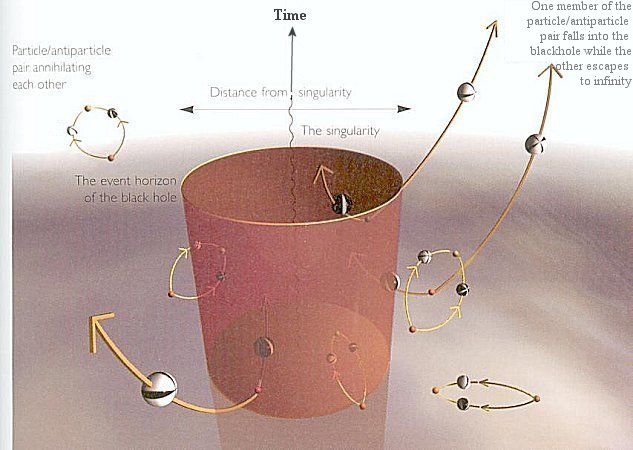
Hawking Radiation Blackhole Evaporation hole is not completely closed to the universe outside. It turns out that vacuum fluctuations at the edge of the event horizon may allow one member of the virtual particle / anti-particle pair to fall inside with negative energy; while the other escapes as a real particle with a positive energy according to the law of energy conservation. This is known as Hawking radiation (see Figure 09u); it is the first successful attempt to combine general relativity and quantum theory. The flow of negative energy or mass into the black hole

Figure 09u Hawking Radiation
[view large image]

Figure 09v Black Hole Evaporation
[view large image]

 would reduce its mass. As the black hole loses mass, the area of its event horizon gets smaller, but this decrease in the entropy of the black hole is more than compensated for by the entropy of the emitted radiation, so that the second law of thermo-dynamics is never violated.

Since T 1 / m, and the rate of radiation L can be expressed as L rs2T4 1 / m2. Therefore, as the black hole loses mass, its temperature and rate of emission increase, then it lose mass even more quickly (Figure 09v). What happens when the mass of the black hole eventually becomes extremely small is not quite clear, but the most reasonable guess is that it would disappear completely in a tremendous final burst of emission.

The temperature T in Eq.(16d) can be expressed in term of solar mass:

T = 0.6 x 10-7 msun / m (in degrees Kelvin)

where msun is the mass of the Sun. If the Sun is reduced to a black hole, its temperature would be just about 10-7 oK. On the other hand, there might be primordial black holes with a very much smaller mass that were made by the collapse of irregularities in the very early stages of the universe. Those with masses greater 1015 gm could have survived to the present day. They would have the size of a proton (~ 10-13cm) and a temperature of 1011 oK. At this temperature they would emit photons, neutrinos, and gravitons in profusion; they would radiate thermally at an ever-increasing rate, and sending out X rays and gamma rays to be discovered. The lifetime of a black hole is roughly equal to = m / L = 10-35 m3 year, where m is in gm. This makes an ordinary mass black hole (m ~ 2x1033 gm for the Sun) live for a long time and its radiation unobservable.

Event Horizon This phenomenon of Hawking radiation also occurs in the event horizon created by an accelerating observer. Figure 09w shows that light ray emitted at certain distance can never catch up with the observer and thus an event horizon exists beyond which the observer cannot communicate. Theoretical arguement suggests that even in empty space, the observer will be able to detect radiation from the event horizon. A simple formula is derived to express the relationship between the acceleration a and the temperature T:

Figure 09w Event Horizon of an Accelerating Observer [view large image]

 T = a (/2kBc). It is suggested that members of the correlated virtual photon pairs are separated by the event horizon. As a result part of the information is missing, the observer detects random motion associated with the temperature. In this case the energy is extracted from the acceleration, which according to general relativity, is equivalent to gravitation.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.