Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Relativity, Cosmology, and Time

Contents

Classical Mechanics
Special Relativity
General Relativity
Schwarzschild's Solution and Black Hole (2018 Edition)
Kerr's Solution and Rotating Black Hole
Black Hole Interior (2019)
A Scenario for Time Travel
Hawking Radiation
Black Hole Information Paradox (2018 Edition)
Standard Cosmology
Hubble Constant and 2018, 2020 Updates
Cosmological Constant and de Sitter Universe
Theory of Cosmic Inflation and Acceleration
Static Universe and Cosmic Acceleration (2021 Edition)
Angular-Size Redshift Relation
Euclidean Space
Five Dimensional Space-time
Gravitational Wave
Un-relativistic Theory
Momentum Space
A Collection on the Ideas about Time

Classical Mechanics

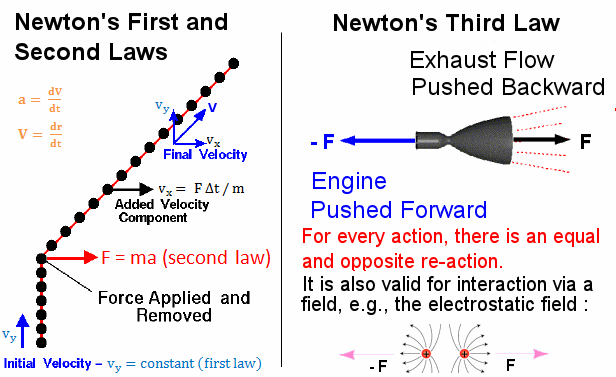
Newton's Laws Classical mechanics describes the way objects move and interact in accordance with Newton's laws of motion (Figure 01a). The basic assumptions involve a frame of reference (x,y,z) with respect to which object with mass m moves, there is an independent time variable t to record the sequence of the movement, the gravitational or electromagnetic interaction between objects is instantaneous, and objects with geometric extent are often idealized as a point (with the justification that the size is much smaller than the distance involved). The basic equation is:

Figure 01a Newton's 3 Laws [view large image]

F = m a ---------- (1)

This formula is known as the equation of motion and looks deceptively simple. However, the force F and acceleration a are vectors, which have to be resolved into the x, y, z components. The acceleration a is the time derivative of the velocity v, which is also a vector and the time derivative of the positional vector r, i.e., v = dr/dt. Eq.(1) is known as Newton's second law, which state: "Acceleration is proportional to the resultant force and is in the direction of this force with the proportional constant equal to the mass". If the positional vector r is decomposed into r = x i + y j + z k, where i, j, and k are unit vectors along the x, y, z axes respectively, then Eq.(1) can be written in its component form:

Fx = m d2x/dt2,    Fy = m d2y/dt2,    and    Fz = m d2z/dt2 ---------- (2)

which are essentially three separate differential equations. Strictly speaking, Eq.(2) is applicable only to a point mass without spatial extent. But it is often used on extended objects such as a brick, the Earth, ... without stating explicitly the idealization. It has created lot of confusion in countless inquiring minds, many of which have eventually developed a phobia for physics. The simplification is valid only if the distance scale is much larger than the size of the object(s). The same kind of problem also occurs in the Big Bang theory which proposes the origin of the universe from a point with infinite density, and in the theory of elementary particles, which is plagued with infinities - the result of treating the particles as points without internal structure.

The force F can be a sum of many forces acting together; if the resultant is zero then the object is said to be in equilibrium and would not experience acceleration. This is the Newton's first law, which read (in its original form): "Everybody continues in its state of rest, or of uniform motion in a straight line, unless its is compelled to change that state by forces impressed on it.".

The Newton's third law is (in his own words): "To every action there is always opposed an equal reaction; or, the mutual actions of two bodies upon each other always equal, and directed to contrary parts." This law implies that interaction is always between two bodies; whenever one body exerts a force on another, the second always exerts on the first a force which is equal in magnitude, opposite in direction, and has the same line of action. A single, isolated force is therefore an impossibility. Sometimes it seems that one body experiences a force without a second body, e.g., a charged particle in the constant electric field of a capacitor; this is because the second body is very heavy, and no appreciable movement is induced by the interaction.

The Newton's law of universal gravitation is in the form:

F = -(Gm1m2 / r2) (r/r) ---------- (3)

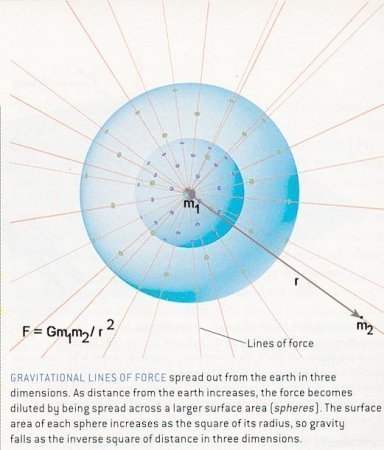Gravitational Interaction where G is the gravitational constant, m1 and m2 are the masses of the two objects interacting via gravitation, r is the distance between these two objects, and (r/r) is an unit vector along the direction of r (see Figure 01b).

If one of the objects is much heavier than the other, e.g., m1 >> m2 like the Sun / Earth system, then m1 can be placed in the origin of the coordinate system and Eq.(1) can be solved as a one-body problem. In case the two masses are similar, the problem can be reduced to a one-body problem with a fictitious object moving around the center of mass, and Eq.(1) is still applicable. The equation of motion becomes rapidly un-manageable for system of three bodies and beyond. Eq.(1) would be applied to all the objects and the force on one object would involve the interaction with all the others. This is the situation often encountered in celestial mechanics with spacecraft flying among planets. The solution is usually obtained by some kind of approximation and by numerical computation using large

Figure 01b Gravitational Interaction

computers. See Newton's Laws in cartoons.


Three-body Problem Actually, Newton's equation of motion for many particles can be expressed in a deceivingly concise form :

F1(r) = m1 d2r1/dt2,    F2(r) = m2 d2r2/dt2,    F3(r) = m3 d2r3/dt2,     ...    Fn(r) = mn d2rn/dt2,
where r stands for the collective location of every particle in the system (and that's where the complication arised), and the subscript 1, 2, 3, ... n are referred to particle 1, 2, 3, ... n. For n astronomical objects interacting by gravity only, the total force acting on the jth object is in the form:
Fj(r) = - Gmjmi(rj - ri)/|rj - ri|3

Figure 01c Three-body Problem

These set of equations are highly non-linear, the motion becomes very sensitive to the initial and boundary conditions even for the case of n = 3 (Figure 01c, click "refresh" to restart the motion).

The problem with classical mechanics started with the speed of light in two inertial frame of reference. Now consider two frames of reference S and S'. The S' system is coincided with S at t = 0 and moving with a constant velocity V along the x axis as shown in Figure 02a. The transformation of coordinates between these two inertial systems (also known as inertial frame of reference in which external force is absent and thus moving body proceeds with constant velocity) can be expressed by the Galilean transformation according to a S' frame observer viewing the S frame :

x' = x - Vt,   y' = y,   z' = z,   and   t' = t ---------- (4)

It is obvious that the length l = x2 - x1 = l ' = x'2 - x'1, i.e., it remains unchanged in the two coordinate systems. In general, the invariant form of the infinitesimal length can be expressed as:

Galilean Transformation d2 = dx2 + dy2 + dz2 = dx'2 + dy'2 + dz'2 ---------- (5)

According to Eq.(4) if the velocity of light (in the x direction) is c in the S frame it would be c' = c - V in the S' (moving) frame. In classical mechanics, the "Absolute Frame of Reference" is a hypothetical entity identified as the frame of reference with the origin at the center of mass of system of fixed stars. Only with respect to this absolute frame of reference would the velocity of light equal to c = 3x1010 cm/sec.

Figure 02a Galilean Transformation

It was later suggested that the medium in which light propagates - the ether - would be an even better absoute frame of reference.
Note: In the subsequent text, V denotes the velocity between inertial frames, and v is the velocity of a point in an inertial frame.

See examples of classical mechanics in "Curvilinear Motions" and "Harmonic Oscillator".

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.