
 in Eq.(18a). Simple mathematics as well as from solution of the equation§ shows that such model describes an expanding universe. In order to avoid this "unwanted" predicament, he introduced a repulsive term
in Eq.(18a). Simple mathematics as well as from solution of the equation§ shows that such model describes an expanding universe. In order to avoid this "unwanted" predicament, he introduced a repulsive term  = 4
= 4 G
G /c2 to make d2R/dt2 = 0. The additional term would make dR/dt = 0 as well if
/c2 to make d2R/dt2 = 0. The additional term would make dR/dt = 0 as well ifk = 4
 G
G R2/c2 or k =
R2/c2 or k =  R2. Thus, R = R0 = constant (see mathematical detail). However, this universe is unstable. A small perturbation would induce collapse or expansion forever. With the discovery of
R2. Thus, R = R0 = constant (see mathematical detail). However, this universe is unstable. A small perturbation would induce collapse or expansion forever. With the discovery of Figure 10l1 Einstein and His Cosmic Blunder
[view large image]
 back into the model universe. The crucial difference is that we now know the density
back into the model universe. The crucial difference is that we now know the density  is not a constant; it varies with time as the universe expands. The two terms on the right-hand side of Eq.(20f) equal to each other only momentarily about 8 billion years after the Big Bang.
is not a constant; it varies with time as the universe expands. The two terms on the right-hand side of Eq.(20f) equal to each other only momentarily about 8 billion years after the Big Bang.


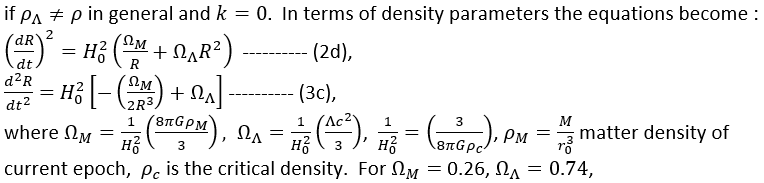


 (R0/2)eHt (as t
(R0/2)eHt (as t  ), the minimum size Rmin = R0;
), the minimum size Rmin = R0; 0), otherwise R0 = R(t = 0) (for k = 0).
0), otherwise R0 = R(t = 0) (for k = 0).