Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Relativity, Cosmology, and Time

Black Hole Interior (2019)

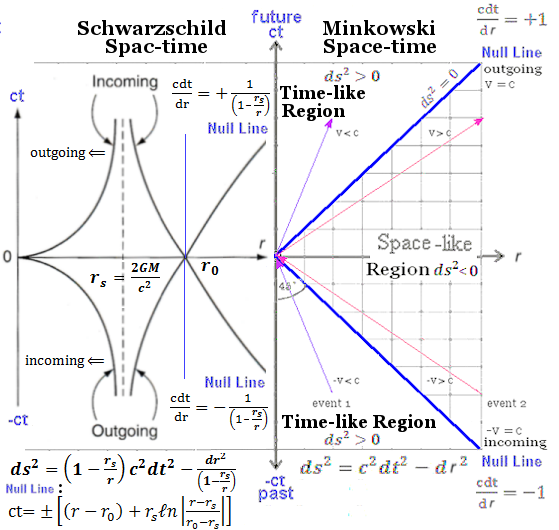
Black Hole Space-time The fate of the collapsing matter in a black hole is supposed to be compressed into a point at infinite density according to conventional wisdom. Other possibilities include : (1) more levels of degeneracy support such as from the quarks (see quark star) or the hypothetical preons (see Preon Star); (2) the unknown effect of quantum gravity, (3) and then the Penrose universes via rotating black hole. Anyway, the Schwarzschild space-time dictates that the event horizon rs separates the space-time into two regions outside and inside rs with distinct properties as shown in Figures 09rd. While the exterior region has found to correspond to many physical features, it is not known if the interior part makes any sense.

Figure 09rd BH Space-time

The following is an attempt to introduce quantum effect into the collapse using the Friedmann equation to describe the metric tensor for the interior of the black hole.

The Robertson-Walker space-time metric for homogeneous and isotropic matter-energy distribution is in the form :

ds2 = c2dt2 - R(t)2 [dr2 + w2 (d2 + sin2 d2)], where w = sin(k1/2 r) / k1/2 with k >, =, < 0 for closed, flat and open space respectively.

This form of space-time metric does not distinguish the inside and outside regions of the black hole. There is no signature change at crossing the event horizon, i.e., no switching of the role of space and time in the space-time metric as suggested by the Schwarzschild metric (see Figure 09rd). Since either one, not both could be the correct description of nature, if the Robertson-Walker space-time turns out to be the more suitable solution for the black hole interior then all the predictions about white hole, worm hole else would become merely a science fiction curiosities.

The Friedmann field equation to determine the metric tensor R(t) with mass M and spatial curvature k included takes the form :

(dR/dt)2 = R2{[2GM / (r03R3)] - kc2/R2} ---------- (1a), or
(dR/dt)2 = c2R2{[(rs/r0) / (r02R3)] - k/R2} ---------- (1b),
where R is the so-called scale factor, r0 the radial coordinate for R = 1, and rs = 2GM/c2 is the Schwarzschild radius.

Eq.(1a) can be quantized as shown in "Quantization of the Friedmann Equation (Matter-only)" for cosmic expansion from a Planck size entity. The formulation is also valid for gravitational collapse.

This equation has two solutions corresponding to |dR/dt|. The positive solution represents the cosmic expansion, while the negative one could describe the collapse of matter in a black hole. Starting from r0 = rs, k = 1/(rs)2 Eq.(1b) becomes :

dR/dt = - (c/rs)[(1/R) - 1]1/2 ---------- (1c).

By imposing the initial time t = 0 for R = 1 at rs, the classical solution is :
Black Hole, Collapse of

Figure 09re Black Hole, Collapse of

(Figure 09rf).
k1 is evaluated with n = 1, the density 1 is estimated by equating to M(k1)3/2. For comparison, the central density of neutron star is ~ 1015 gm/cm3 and ~ 10220 gm/cm3 at the beginning of the inflation period.
See Figure 09re for a visual description.

Black Holes, 3 Kinds
where nq = (M/MPL)2(rq/rs) is the quantum number at the classical to quantum matching point, i.e., (1/Rqrs)2 = (M/MPL)4(1/nqrs)2; while kq ~ 1014 cm-2, and tq ~ (rs/c)[(/2) - (rq/rs)3/2/2] for rs >> rq.

Figure 09rf Black Holes, 3 Kinds [view large image]

 There is a large range of estimated mass for the hypothetical primordial black hole.


Actually, similar to the Schrödinger equation for hydrogen atom (on which this analysis is based) spontaneous transitions from higher to lower quantum level is not explainable in the quantized version of the gravitational collapse since there is no mixture (no perturbation)
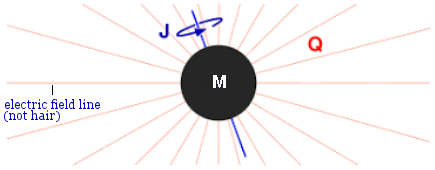No-Hair Theorem between the wave functions of the excited state and the ground state (see example in "QM Basic"). Thus, the collapse may halt at the moment of transition to quantum domain or there is some kind of unknown mechanism that allows the transition to ground state to proceed. Anyway, the derivation up to this point depends on only one independent parameter, e.g., the mass M. The subsequent development and structure follow the specification of just this one variable, no other details are required - the triumph of the "No-hair Theorem" (Figure 09rg) postulated some 50 years ago.

Figure 09rg No-Hair Theorem [view large image]

 BTW, for a test particle with mass m, the escape velocity is determined by (mv2/2) > (GmM/r) giving
v > c inside the region r < rs which is the definition of a black hole, i.e., not even light can escape from inside the region. Thus, such criterion can be derived without referring to the Schwarzschild metric.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.