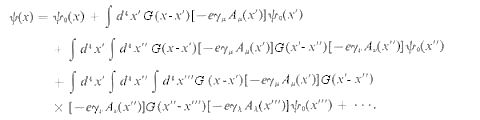
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
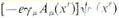 , where A
, where A is the electromagnetic vector potential and
is the electromagnetic vector potential and  is the 4 components spinor separated into 2 parts (in Dirac representation,
is the 4 components spinor separated into 2 parts (in Dirac representation,  and
and  together form a 4-components field for either the fermion or anti-fermion; while in chiral representation they stand for the left-handed and right-handed fermions called Weyl spinors). In term of the Green's function (with
together form a 4-components field for either the fermion or anti-fermion; while in chiral representation they stand for the left-handed and right-handed fermions called Weyl spinors). In term of the Green's function (with  (y) replaced by the interaction term,
(y) replaced by the interaction term,  replacing
replacing  , and G defined by Eq.(9a)), the function
, and G defined by Eq.(9a)), the function  now appears on both sides in Eq.(8). The equation can be solved by an iteration procedure yielding a sum of integrals as shown in the formula below:
now appears on both sides in Eq.(8). The equation can be solved by an iteration procedure yielding a sum of integrals as shown in the formula below:
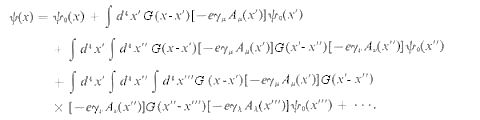 |
---------- (10) |
 0, and the integration is over all the space-time x', x'', x''', ... Note that each of the following term is multiplied by the power of e, from e1, to e2, ... Since e2=1/137 for the electromagnetic interaction, computation on a few terms would be sufficient to obtain a result with acceptable accuracy.
0, and the integration is over all the space-time x', x'', x''', ... Note that each of the following term is multiplied by the power of e, from e1, to e2, ... Since e2=1/137 for the electromagnetic interaction, computation on a few terms would be sufficient to obtain a result with acceptable accuracy. |

 d3x, where
d3x, where  is the Hamiltonian density. The green's function and S-matrix formulations are equivalent since the transition probability amplitude
is the Hamiltonian density. The green's function and S-matrix formulations are equivalent since the transition probability amplitude 
 f(t)|
f(t)| i(t)
i(t) in the former case is the same as
in the former case is the same as  f|S|i
f|S|i =
= 
 f|S|
f|S| i
i in each term of the expansion. The difference in appearance is due to different representation on placement of the time dependent Hamiltonian HI. While the Green's formulation follows the Schrodinger picture with time residing in the wave function; the time-dependence part is within the S-matrix operator itself by adopting the Heisenberg picture. The difference is readily apparent by considering the source and interacting Hamiltonian to be independent of time, e.g., equals to H. By equating the ti's to t, and performing a time-order re-arrangement, it can be shown that Eq.(10) becomes
in each term of the expansion. The difference in appearance is due to different representation on placement of the time dependent Hamiltonian HI. While the Green's formulation follows the Schrodinger picture with time residing in the wave function; the time-dependence part is within the S-matrix operator itself by adopting the Heisenberg picture. The difference is readily apparent by considering the source and interacting Hamiltonian to be independent of time, e.g., equals to H. By equating the ti's to t, and performing a time-order re-arrangement, it can be shown that Eq.(10) becomes  (t) = e-iH(t-t0)
(t) = e-iH(t-t0) (t0), while Eq.(11) turns into S = e-iH(t-t0).
(t0), while Eq.(11) turns into S = e-iH(t-t0).
 f|S|i
f|S|i of the expansion are taken between the initial state (i) at t0 = -
of the expansion are taken between the initial state (i) at t0 = - and the final state (f) state at tn = +
and the final state (f) state at tn = + . Usually, one initial state can produce one or more final states as shown in Figure 01g, where three different initial states are taken as examples - namely, the electron positron scattering, the Compton scattering and the deep inelastic scattering. Each of this process produces many final states, but only a few have been shown just for illustration purpose. The Sfi is a complex number in general. It is called probability amplitude and is related to the probability of going from the i to f states. It has to satisfy the unitary condition, i.e.,
. Usually, one initial state can produce one or more final states as shown in Figure 01g, where three different initial states are taken as examples - namely, the electron positron scattering, the Compton scattering and the deep inelastic scattering. Each of this process produces many final states, but only a few have been shown just for illustration purpose. The Sfi is a complex number in general. It is called probability amplitude and is related to the probability of going from the i to f states. It has to satisfy the unitary condition, i.e.,
 |
 f S*fiSfi = 1, which guarantees that probability is conserved in the process. Such relationship indicates that the matrix Sfi has an inverse, which in turn implies that it is possible to return to the initial state from the final state at least in principle although the probability is almost zero in practice so that the second law of thermodynamics is "almost" never violated. This property is also related to the conservation of information, which caused so much trouble for Stephen Hawking. f S*fiSfi = 1, which guarantees that probability is conserved in the process. Such relationship indicates that the matrix Sfi has an inverse, which in turn implies that it is possible to return to the initial state from the final state at least in principle although the probability is almost zero in practice so that the second law of thermodynamics is "almost" never violated. This property is also related to the conservation of information, which caused so much trouble for Stephen Hawking.
|
Figure 01g S-Matrix |
 |
---------- (12) ---------- (13) |
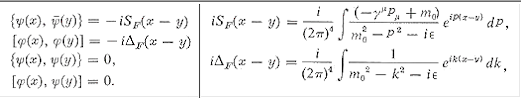 | ---------- (14) |

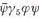 d3x the nth order term in the S-matrix expansion Eq.(11) has the explicit form:
d3x the nth order term in the S-matrix expansion Eq.(11) has the explicit form: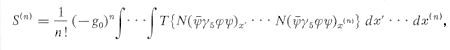 | ---------- (15) |
 to +
to + over all space-time,
over all space-time, 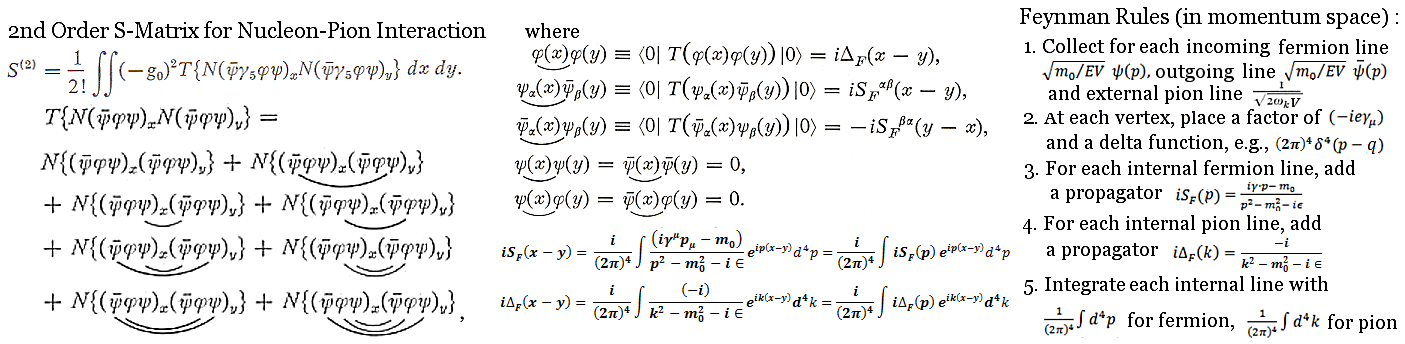
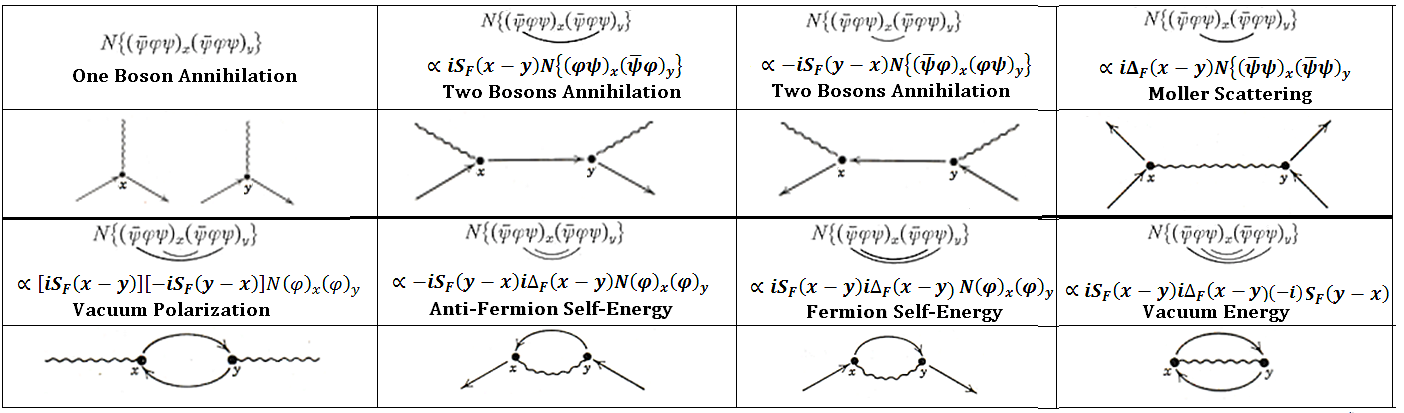
 |
 |
The s-channel corresponds to two incoming particles with 4-momenta p1 and p2, which combine into an intermediate (virtual) particle with real mass and finally emerge as two outgoing particles with 4-momenta p3 and p4 (Figure 01h,a). Mathematically, s = (p1 + p2)2 = (p3 + p4)2 = 4E2, where we assume they all have energy E to simplify the formula. In t-channel, particle with p1 emits virtual particle with imaginary mass, which is absorbed by p2. They depart with p3 and p4 respectively (Figure 01h,b). Thus, t = (p1 - p3)2 = (p4 - p2)2 = 2E2(1 - cos  ), where ), where  is the angle between is the angle between
|
Figure 01h Scattering Channels |
Figure 01i Regge Trajectory [view large image] |
p1 and p3. There is an additional u-channel with the role of particles 3, 4 interchanged. Together they form an identity : s + t + u =  i=1,4 mi2. i=1,4 mi2.
|
 . As shown by QED, it has a logarithmic divergence for J = 1, and becomes nasty unrenormalizable divergence for J > 1 (e.g., for the case of graviton).
. As shown by QED, it has a logarithmic divergence for J = 1, and becomes nasty unrenormalizable divergence for J > 1 (e.g., for the case of graviton). =
=  (0) +
(0) +  ' s, where
' s, where  = J whenever s = m2 and
= J whenever s = m2 and  ' ~ 1/(Gev)2 is the Regge slope (Figure 01i).
' ~ 1/(Gev)2 is the Regge slope (Figure 01i). |
For scalar particles at high energy the scattering amplitude can be generalized to : A(s,t) = -  J gJ2(s)J/(t - mJ2) for the t-channel, and similarly J gJ2(s)J/(t - mJ2) for the t-channel, and similarlyA(t,s) = -  J gJ2(t)J/(s - mJ2) for the s-channel. J gJ2(t)J/(s - mJ2) for the s-channel.The finite summation in these formulas yields values way above the experimental data (Figure 01j). Then it was suggested that an infinite sum may offer a more acceptable result. At about the same time, there were hints that the scattering amplitudes from the two different channels may be equal to each other, i.e., A(s,t) ~ A(t,s), which is now known as the "duality" hypothesis. |
Figure 01j Hadron Scattering [view large image] |
 |
Then a scattering amplitude (known as the Veneziano Amplitude) that satisfies all the stringent requirements of the S-matrix Theory (except the unitarity but including the duality) was discovered in 1968 :
|
Figure 01k Gamma Function [view large image] |
Some comments on the Veneziano amplitude : |
 |
|
Figure 01l Euler Beta Function [view large image] |
 |

|
Figure 01m N-point Amplitude [view large image] |
  |
 |
The necessity of having to devise the N-point amplitude is related to the behavior of hadron collision at very high energies. At about 50 times the rest mass energy of the proton, the dominant feature of most events is the sheer number of particles produced. This number is called the multiplicity of the reaction as shown by Figure 01n, in which the number of the product n for the various species is plotted against the squared energy. BTW, the intermediate particles in the S-matrix theory now include all those in the Regge trajectories. This is referred to as Reggeon exchange, which represents the exchange of all the resonances with different masses and spins. It is similar to the mediation by photon in the electromagnetic interaction. The resonances are referred to as hadron excited states in QCD. |
Figure 01n Multiplicity |
 s2/t, which is hopelessly un-renormalizable. However, this is not so with the Veneziano amplitude. Therefore, it remains to be a potentially correct description for graviton and particles of "excessively high spin" in quantum gravity.
s2/t, which is hopelessly un-renormalizable. However, this is not so with the Veneziano amplitude. Therefore, it remains to be a potentially correct description for graviton and particles of "excessively high spin" in quantum gravity.